אחרי 35 שנה: פתרון לבעיית השלשות הפיתגוריות
במשך יותר משלושה עשורים ניסו מתמטיקאים למצוא את התשובה. לאחר שנמצאה מסתבר שייקח 10 מיליארד שנים לקרוא את ההוכחה. בראיון לאולפן ynet מסביר פרופ' עוזי וישנה מה הבעיה ולמה היא מסובכת
אתם בדיוק שוברים את הראש כדי לפתור תרגיל במתמטיקה? תתנחמו בזה שלפחות תגיעו לפתרון בפחות מ-35 שנה, שזה בדיוק הזמן שלקח לפתור בעיה מתמטית ותיקה, בעיית השלשות הפיתגוריות. ביום שישי האחרון סוף סוף הצליחו להגיע לתשובה, אלא שאז התעוררה בעיה אחרת, כדי לקרוא את ההוכחה תזדקקו לקצת יותר זמן, עשרה מיליארד שנים בערך.
פרופ' עוזי וישנה, ראש המחלקה למתמטיקה באוניברסיטת בר אילן, הסביר על התרגיל: "מתחבאים כאן שני סיפורים, אחד קשור לתורה כללית בקומבינטוריקה, שעוסקת בשאלה האם מערכת מאוד מסובכת ולא מסודרת חייבת להכיל איזשהי מידה של סדר ומסתבר שכן, זה בעצם המשפט שהוכיחו כאן וזה מתחבר לסידרה ארוכה של משפטים מאוד יפים בתחום הזה. הסיפור השני הוא העניין של איך לכתוב הוכחה לטענה כזאת ופה העסק מסתבך ומסביר למה זה לוקח כל כך הרבה זמן".
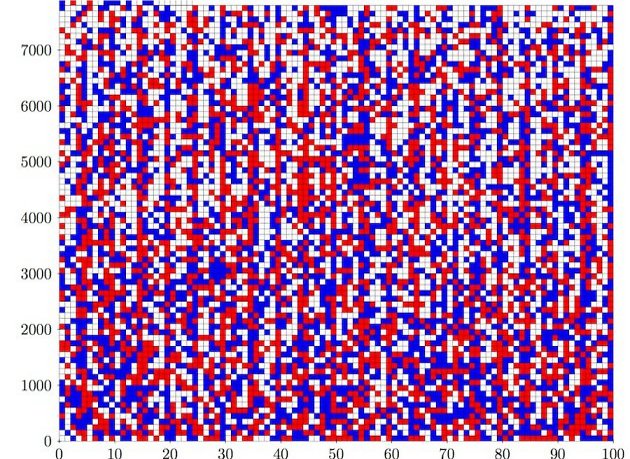
ולמה ייקח 10 מיליארד שנים לקרוא את ההוכחה? פרופ' וישנה מסביר: "שלשה פיתגורית זו שלשה של מספרים שלמים, שמהווים צלעות של משולש ישר זווית, כמו במשפט פיתגורס. השאלה היא פשוטה, האם אנחנו יכולים לצבוע את המספרים הטבעיים בשני צבעים, אדום וכחול באופן כזה שנצליח להימנע מלצבוע שלשה פיתגוריות באותו צבע. כלומר 3,4 ו-5 מהווים שלשה, אסור לצבוע את שלושתם באותו צבע. 5,12 ו-13 הם שלשה, אסור לצבוע אותם באותו צבע, אז יש לנו אינסוף מקומות לבחור באיזה צבע להשתמש, אינסוף אילוצים של שלשות, האם אפשר לצבוע כך שלא נצטרך לצבוע את אותה שלשה באותו צבע, והתשובה היא שאי אפשר".
לדבריו, "מסתבר שאם נרצה לצבוע את המספרים מ-1 ועד 7,824 ולהימנע משלשות פיתגוריות אז זה אפשרי, אבל אם נרצה לצבוע את המספרים מ-1 עד 7825 באותם אילוצים זה כבר בלתי אפשרי. ובמדעי המחשב התפתח תחום של תורת ההוכחות, איך אפשר להציג הוכחה פורמלית לטענה באופן כזה שתוכל לבדוק אותה למרות שאתה לא עובר בעצמך על כל הפרטים של ההוכחה. מה שאני חושב שתלמידי המתמטיקה שנבחנים בבגרות היו שמחים לשמוע, אם הם היו יכולים לכתוב משהו בדף שישכנע שמגיע להם 100 בלי לכתוב את כל הפרטים של ההוכחה - זה היה מצויין. החסרון הוא בדרך כלל ההוכחה שאתה יודע להוכיח לוקחת הרבה יותר מקום מאשר ההוכחה עצמה. זו הסיבה שבמקר הזה ההוכחה הפורמלית של הטענה על 7825 תופסת משהו כמו 200 טרה-בייט של מידע, שזה לא נגיש לבני אדם. זו עבודה למחשבים, בני אדם לא באמת עוסקים בפרטים האלה".
 לפנייה לכתב/ת
לפנייה לכתב/ת 










