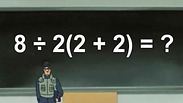על הפסיכולוגיה של המתמטיקה

לאחרונה סערה הרשת בעקבות תרגיל פשוט בחשבון. נדמה שאין איש שלא ניסה את כוחו בחישוב הביטוי הפשוט הבא: 

התרגיל שעורר מחלוקת ברשת(איור: מתוך טוויטר)

אם במקרה התרגיל הזה לא פגש אתכם עד עכשיו ברשת, עצרו רגע ונסו לחשב!

מספר לא מבוטל של מגיבים, כולל כאלו שמצהירים על עצמם כבעלי ידע ברמה אקדמית במתמטיקה, חישבו ומצאו שהתשובה היא 1. לעומתם, יש שמציעים להם לדרוש את כספם בחזרה מהאוניברסיטה (ואולי מבית הספר היסודי) וטוענים בתוקף שהתשובה היא 16.

בימים האחרונים הדיון בשאלה חצה את גבולות הפורומים לגיקים. ה"ניו יורק טיימס" פרסם כתבה של האדם שיודע לכתוב וללמד מתמטיקה כאילו מדובר בשירה, פרופ' סטיבן סטרוגטס. בטור מנומק מסביר סטרוגטס שאומנם מבחינה מתמטית טהורה התרגיל לא מוגדר היטב, כך שגם אם בחרתם בתשובה ה"לא נכונה" תוכלו להרגיש בנוח, אך על פי המוסכמות הנהוגות התוצאה המקובלת היא 16, כיוון שהפעולות כפל וחילוק שקולות מבחינת סדר פעולות החשבון ומכיוון שאנו פותרים משמאל לימין.

מה גרם לאנשים רבים כל כך לבחור את הפתרון הלא מקובל לתרגיל פשוט כל כך, האם זה חוסר הידע הנהוג בסדר פעולות חשבון? או שאולי סיבה אחרת, שנובעת ממבנה התרגיל המיוחד הזה היא שגרמה לטעות. האם ייתכן שהתרגיל הפשוט, לא "תמים" בכלל?

ראשית, שימו לב לסוגריים. הם ממקדים את תשומת הלב שלנו בצד ימין. שנית, נשים לב שלא מופיע סימן הכפל בין השתיים שכופל את הסוגריים, לסוגריים עצמם. החלק הזה של הביטוי הוא לא "2 כפול 2+2", אלא כביכול "פעמיים 2+2". אמנם זה "כשר למהדרין" מבחינה מתמטית, אבל עלול "לדחוף" את הפותר לבצע מיידית את פעולת הכפל.

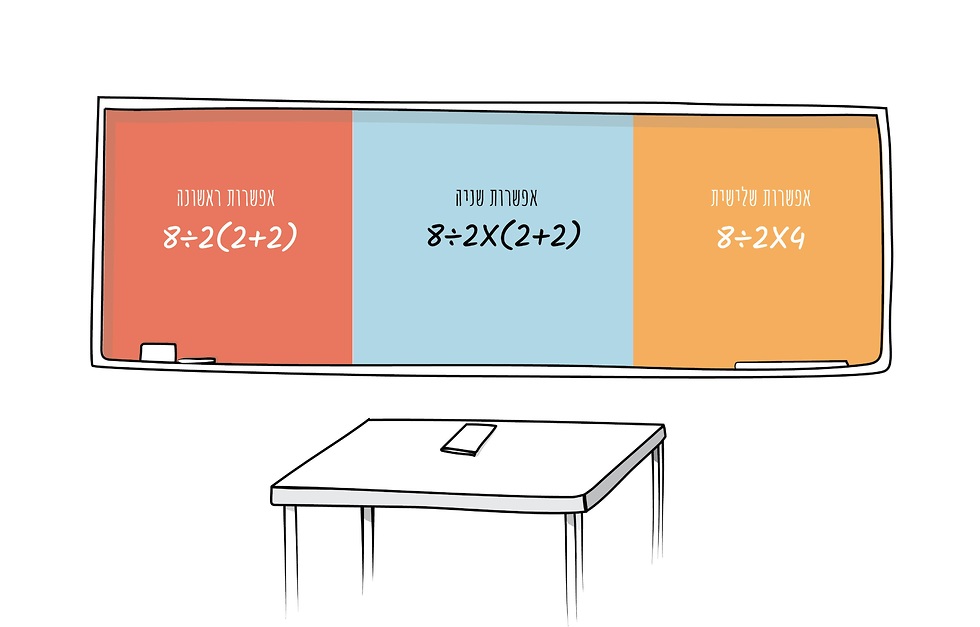
על מנת לבדוק את הסיבה לבחירה באחד הפתרונות, ערכנו ניסוי שבו השתתפו 61 סטודנטים בעלי רקע זהה במתמטיקה. כולם נבחנו ב-5 יח"ל במתמטיקה, הם בעלי ציון פסיכומטרי גבוה, ועומדים ללמוד באוניברסיטה במחלקות לפיסיקה והנדסה. כל סטודנט התבקש לפתור בתוך 10 שניות אחד משלושת התרגילים הבאים:

השאלות(איור: ד"ר יוסי בן ציון)

לכל התרגילים תוצאה זהה, 16, אך בעוד שהאפשרות הראשונה זהה לתרגיל המקורי, באפשרות השנייה הוספנו את סימן הכפל באופן מפורש, אך השארנו את הסוגריים ובאפשרות השלישית גם הוספנו את סימן הכפל וגם הורדנו את הסוגריים.

אם אין פה תעלול "פסיכולוגי", נצפה שהתפלגות התשובות תהיה דומה בשלוש הקבוצות. כלומר אם בעיית הפותרים באופן הלא מקובל היא חוסר ידע (או שכחה) של סדר פעולות החשבון הרי שאין הבדל בין שלוש האפשרויות.

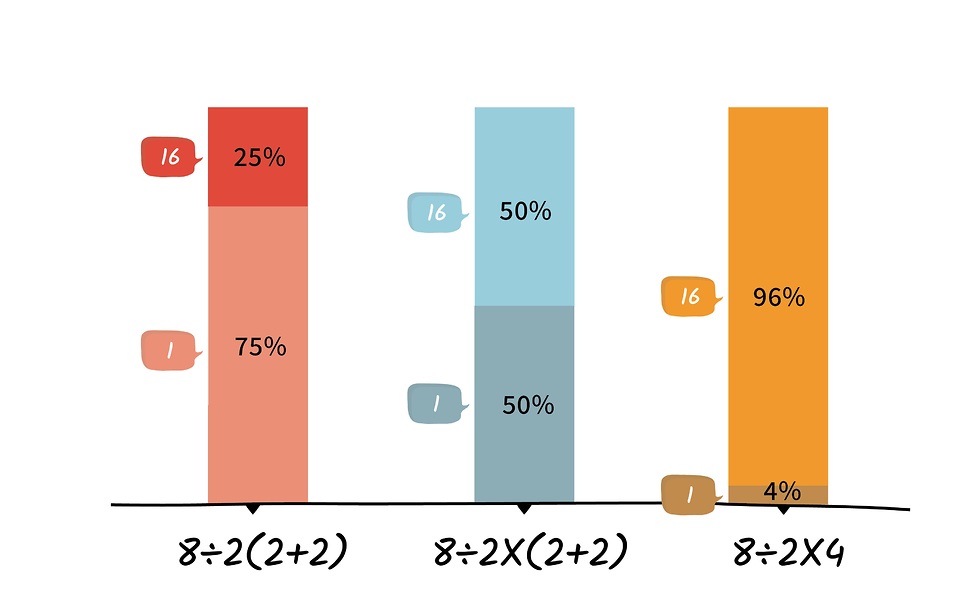
התוצאות חד משמעיות. הסטודנטים שקיבלו את האפשרות השלישית בחרו בפתרון המקובל: 24 סטודנטים מתוך 25 ענו 16 ורק אחד ענה 1.

הסטודנטים שקיבלו את האפשרות הראשונה, התרגיל המקורי "התמים", הציגו תוצאה מפתיעה למדי, 15 מתוך 20 ענו שהתוצאה היא 1, ורק 5 בלבד ענו 16.

התלמידים שקיבלו את האפשרות השנייה, הזהה לאפשרות הראשונה, פרט לתוספת סימן הכפל לפני הסוגריים, הציגו שיפור משמעותי: 8 מתוך 16 ענו את התשובה הנכונה, 16, ומספר זהה טעה וענה 1.

התפלגות התוצאות(איור: ד"ר יוסי בן ציון)

המסקנה מהניסוי היא שהמורים שלנו עשו עבודה טובה מאוד בבית הספר היסודי. ללא ספק הסטודנטים שולטים בסדר פעולות החשבון ובמוסכמה לפתרון משמאל לימין כפי שהציגו הפותרים של האפשרות הראשונה. הכשל הוא "אנושי", בעזרת "מלכודת תשומת לב" בדמות סוגריים והעדר (חוקי) של סימן הכפל, התרגיל "התמים" יצר מניפולציה על הדרך שבה אנחנו רואים את התרגיל ופותרים אותו.

על מנת להיות ממש בטוחים, ערכנו ניסוי נוסף. כשעה לאחר שסיימנו את הניסוי הראשון התבקשו אותם סטודנטים לפתור תוך 10 שניות נוספות את התרגיל הבא: 6:3X2 מתוך 23 שפתרו לא נכון (על פי המוסכמות) בקבוצת האפשרות הראשונה והשנייה, 18 פתרו באופן מדויק כך שאת סדר פעולות החשבון הם יודעים. מה שגרם לטעות המקורית, כאמור, הוא אופן הצגת התרגיל.

ד"ר יוסי בן-ציון, המחלקה לפיסיקה אוניברסיטת בר אילן