הכי ממשיים שיש: הכירו את המספרים המרוכבים

המספרים המרוכבים צצו במאה ה-16 באיטליה, כחלק ממרוץ החימוש שניהלו מתמטיקאים איטלקיים זה נגד זה בקרב הגדול – מי פותר משוואות טוב יותר.

למשוואות ממעלה שניה, מהסוג שלומדים בחטיבת הביניים, הייתה נוסחה פשוטה, אך עבור משוואות ממעלה שלישית ומעלה האתגר היה גדול בהרבה. גם משנמצאה נוסחה לפתרון משוואה ממעלה שלישית, היא הכילה בתוכה מלכוד מוזר; כחלק מתהליך הפתרון לעתים לא היה מנוס מלהשתמש בשורש הריבועי של מינוס 1.

ומדוע זה מוזר? מכיוון שאנו רגילים לכך שלמספרים שליליים אין שורש ריבועי. 3 הוא השורש הריבועי של 9, שכן כאשר כופלים את 3 בעצמו מקבלים 9; גם אם כופלים את מינוס 3 בעצמו מקבלים 9, שכן כפל מספר שלילי במספר שלילי מניב מספר חיובי. אם כן, איך יכול להתקבל מספר שלילי על ידי כפל של מספר כלשהו בעצמו?

השורש של מינוס 1 בהכרח היה צריך להיות יצור חדש, מספר שכמותו טרם ראתה המתמטיקה; לימים הוא יסומן באות i, קיצור למילה imaginary – "מספר דמיוני", כפי שהפילוסוף והמתמטיקאי רנה דקארט אמר עליו בזלזול.

אם כן, i הוא מספר שמקיים i בחזקת 2 =1-, והוא מציב בפנינו כמה שאלות: האם הוא קיים בכלל? מהן ההשלכות של הכנסתו למשחק המתמטי? האם בכלל יש בו טעם מעבר לכלי לפתרון משוואות מסויימות?

מספרים ממשיים: לא מה שחשבתם

אודה ואתוודה: כשאני שומע מה אנשים אומרים לפעמים על i אני מתעצב מאוד. "מספר חסר הגיון לגמרי", "המצאה של מתמטיקאים מטורפים", "לא קשור למציאות" ועוד שלל עלבונות שמוטחים בו. עם זאת, בשלב ראשון לא ארצה לעורר בכם, הקוראים, אמונה בכך שהמספר הזה לגיטימי. יותר מכך: אני רוצה להתחיל בלנפץ דעות קדומות שאולי קיימות אצלכם לגבי לגיטימיות של מספרים אחרים – המספרים ה"ממשיים".

הבה ונחזור לכיתה א'. המספרים הבסיסיים ביותר הם אלו שמככבים ב"אחד מי יודע" – אחד, שתיים, שלוש, ארבע... וכך עוד ועוד. המספרים הללו מכונים "המספרים הטבעיים", שכן מבין כל המספרים הם אכן אלו שצצים באופן טבעי גם בתרבויות פרימיטיביות (אף כי עצם הרעיון של "מספר" – כלומר, שזוג תפוחים וזוג ילדים מקיימים איזו תכונה זהה של כמות – איננו רעיון פשוט כלל).

כבר עכשיו ייתכן שחלקכם שואלים: איפה האפס? האם הוא איננו מספר טבעי? והתשובה איננה פשוטה – במשך מאות ואלפי שנים האפס היה מוקצה או מקובל בערבון מוגבל כמעט בכל מקום! והנה לנו כבר מספר יומיומי שנתון לפקפוק.

בבית הספר היסודי אנו לומדים את פעולות החשבון הבסיסיות שניתן לבצע במספרים הטבעיים - חיבור, חיסור, כפל וחילוק - ומייד צצות בעיות גם כאן. שמונה פחות שלוש הוא חמש, את זה כולם יודעים; אבל מה זה שלוש פחות שמונה? אין מספר טבעי שמהווה את הפתרון לשאלה הזו, ועצם העובדה שבכלל יכול להיות "משהו" שמתאים לשלוש פחות שמונה יכולה להיראות מוזרה בנסיבות המתאימות.

בדיחה ידועה מספרת על מתמטיקאי שצופה בכניסה לבניין – קודם נכנסים לבניין שני אנשים, ולאחר מכן יוצאים ממנו שלושה. "אם עכשיו ייכנס אליו אדם נוסף", אומר המתמטיקאי, "הבניין יהיה ריק".

המצאת המינוס

אנחנו פותרים את בעיית השלוש-פחות-שמונה על ידי "המצאת" מספרים חדשים – מספרים שליליים. אנו קוראים לתוצאה "מינוס חמש", אבל האם אנו רואים מינוס 5 הולך ברחוב, כמו שאנו רואים חמישיות של שחקני כדורסל על המגרש?

מינוס מופיע לנו (למרבה הצער) בחשבון הבנק, בקומות בניין, בגובהו של ים המלח ביחס לפני הים, או במעלות החום בארצות שאינן ישראל. בכל המקרים הללו יש אספקט מלאכותי כלשהו, של נקודת ייחוס מעשה ידי אדם שממנה מתבצעת המדידה.

אין הכוונה, כמובן, שהמספרים השליליים אינם לגיטימיים או חוקיים (אף כי במהלך ההיסטוריה גם טענות כאלו הועלו); להיפך, אלו מספרים נפלאים ושימושיים ביותר כפי שהדוגמאות שהבאתי מראות. אני רק רוצה להצביע על כך שמה שנתפס בעינינו כ"המצאה שרירותית" מתחיל כבר כאן.

בעיות חילוק

בבעיה דומה אנו נתקלים גם בחילוק. שישה תפוחים לחלק לשני ילדים פירושו שכל ילד מקבל שלושה תפוחים. אבל מה קורה אם רוצים לחלק לשני הילדים חמישה תפוחים? התשובה שלנו "שני תפוחים וחצי" נדמית טבעית מאוד כי כבר התרגלנו לעבוד עם שברים כשם שאנו רגילים לעבוד עם מספרים שליליים, אבל גם השברים עצמם הם המצאה שלנו.

אמנם, הם קצת יותר מוחשיים מאשר מספרים שליליים: אנו יכולים להעלות בדעתנו "חצי תפוח". מצד שני, גם כאן אנחנו נתקלים בבעיות. למשל, בכל פעם שבה חוצים תפוח לשניים חצי אחד קצת יותר גדול, או קצת יותר טעים (ולכן לא זהה לחצי השני), ובוודאי שקשה להעלות על הדעת בעזרת פירוק תפוחים שברים מורכבים יותר כמו "17,325 חלקי 31,543 תפוח".

למרות הבעיות הקטנות הללו, השברים – שנקראים גם "המספרים הרציונליים" – הם דוגמה למספרים מומצאים שמסתדרים לנו היטב בתפיסת המציאות. הם מרחיבים לנו בצורה פשוטה ונאה את מערכת המספרים הטבעיים – כלומר, המספרים הטבעיים הם בעצמם חלק ממערכת המספרים הרציונליים (כל מספר טבעי הוא בעצמו שבר עם 1 במכנה).

הסודות של פיתגורס

בתקופת יוון העתיקה, פיתגורס וחסידיו סברו שניתן לתאר את היקום כולו באמצעות מספרים רציונליים עד שגילו לזוועתם כי קיימים מספרים שאינם רציונליים כלל; המפורסם שבהם הוא ללא ספק שורש שתיים, שפשוט אין שום דרך להציגו כמנה של שני מספרים שלמים (קיימת לכך הוכחה נפלאה ששולי מאמר זה צרים מלהכילה, אך היא אינה דורשת יותר ממספר שורות).

האגדות מספרות כי הפיתגוראים כה הזדעזעו מכך שהמספרים הרציונליים שלהם כשלו כל כך בתיאור המציאות עד שניסו לשמור את התגלית בדבר קיומם של מספרים לא רציונליים בסוד והטביעו (!) אחד משלהם שחשף את הסוד הנורא לעולם.

אבל רגע אחד. אמרתי ש"שורש שתיים אינו רציונלי". טוב ויפה, אז למה שורש שתיים קיים בכלל? בינתיים הסכמתי לקבל את קיומם של מספרים טבעיים, מספרים שליליים, מספרים רציונליים... לא הסכמתי בשום מקום לקבל את קיומם של מספרים אחרים.

תגידו – נו, אבל זה השורש של שתיים! מספר שכשמעלים אותו בריבוע מקבלים שתיים! מה הבעיה כאן? אפילו סימון יפה יש לנו: 2√. וגם בבית הספר תמיד הוצאנו שורש לשתיים בלי לשאול שאלות. אז איך אתה מעז לטעון שיש כאן בעיה?

אני לא טוען, חלילה, שיש כאן בעיה: רק שאת ההגיון שאתם מפעילים כאן, כדאי להפעיל גם על השורש המושמץ של מינוס 1. צריך להבין ששורש שתיים הוא רק תחילת הסיפור – כל שורש של מספר שאינו ריבוע (למשל 3,5,6,7,8,10 וכן הלאה) איננו רציונלי; וגם קבועים מתמטיים מפורסמים כמו פאי (π) אינם רציונליים. למעשה, רוב המספרים שבבית הספר מכנים "מספרים ממשיים" אינם רציונליים.

אלא שלאותם מספרים ממשיים יש יתרון עצום על i שלנו בקרב על פיוס האינטואיציה שלנו – הגאומטריה. שורש שתיים הוא אורכו של האלכסון בריבוע שאורך צלעו 1 (זוהי תוצאה של משפט פיתגורס), ואילו π הוא היקף של מעגל שאורך קוטרו 1. כלומר, אלו הם אורכים שקל לנו להעלות על הדעת בעולם האמיתי, גם אם בפועל לא ברור אם אנו מסוגלים לבנות אותם (שהרי בחיים האמיתיים רמת הדיוק שלנו במדידה היא תמיד מוגבלת, ואילו מספרים שאינם רציונליים דורשים דיוק מדידה אינסופי).

בבית הספר המספרים הממשיים זוכים להגדרה המעורפלת "כל המספרים שעל גבי ציר המספרים". זה סוגר את העניין מבחינתנו, כי מה יכול להיות יותר ממשי וקונקרטי מאשר קו ישר של מספרים? ובכל זאת, מתעורר ספק: מה מבטיח לנו שעל גבי הציר הזה יהיה מספר שכשכופלים אותו בעצמו מקבלים 2? עצרו רגע וחשבו על כך.

פרט לכך שהתרגלתם אולי לכך שהמספר הזה קיים, שום דבר לא מבטיח לכם את זה, אבל אנחנו "יודעים" שהוא צריך להיות קיים כי אנחנו מעלים בדמיוננו אובייקט מתמטי אחר, שאיננו ציר המספרים, שבו הוא מופיע – אותו ריבוע עם אורך צלע 1. בגלל תופעות כאלו אנחנו משתכנעים שציר המספרים חייב להכיל יותר מאשר רק את המספרים הרציונליים. אבל בבית הספר לא ממש מתייחסים לבעייתיות הזו ובוודאי שלא פותרים אותה.

בדרך לאינסוף

פתרון אחד נעוץ בפיתוח העשרוני של מספרים. את המספר חצי כותבים בפיתוח עשרוני בתור 0.5, ואת שלוש שמיניות כותבים בתור 0.375, וכל שבר אפשר לכתוב באופן דומה.

קיימים שברים מסויימים, כמו שליש, שהפיתוח העשרוני שלהם הוא אינסופי; הפיתוח של שליש, כפי שכל מי שהשתעשע עם מחשבון ודאי יודע, הוא ...0.333, כאשר שלוש הנקודות אומרות "זה לא נגמר כאן! זה ממשיך לנצח".

לפיתוח עשרוני אינסופי מוזרות קטנה: את המספר 1 ניתן לכתוב גם כ-...0.999 – זהו שוויון ממש ולא "שאיפה ל...", וובעצם כל פיתוח עשרוני שנגמר באינסוף ספרות של 9 ניתן להחליף בפיתוח סופי של אותו המספר בדיוק. פרט למוזרות הזו פיתוחים עשרוניים מתנהגים נחמד למדי.

ובכן, אומרים המתמטיקאים, כל פיתוח עשרוני, אינסופי או סופי, מגדיר לנו מספר; המספרים הממשיים יהיו כל המספרים שיש להם פיתוח עשרוני שכזה. שורש שתיים, למשל, הוא ... 1.4142, רק שכאן שלוש הנקודות הן מסוכנות: המספר נמשך עוד ועוד לנצח, אבל להבדיל מ-...0.333, שהוא מספר שנמשך "עד אינסוף" אבל מספיק לכתוב מספר סופי של סדרות כדי שהחוקיות שבו תוצג במלואה, כאן אין חוקיות שאפשר לעקוב אחריה, אין ספרה שפשוט חוזרת על עצמה שוב ושוב, וזוהי תכונה כללית שמאפיינת מספרים לא רציונליים.

זה אומר שלהבדיל מכל המספרים שדיברנו עליהם עד עכשיו, לחלק מהמספרים הממשיים אין ייצוג עשרוני סופי. כדי לכתוב את כל הספרות של חלק מהמספרים הממשיים, אני חייב לכתוב אינסוף ספרות. מושג ה"אינסוף", שהוא מושג מתמטי מרכזי ומרתק, אך גם בעייתי, תוקע כך טריז באמצע עולם המספרים שלנו.

אין זה אומר שאין דרך אחרת לייצג את שורש שתיים באופן סופי כלשהו – תוכנית מחשב שמחשבת אותו (יש כזו) היא דוגמה לייצוג סופי שכזה (הייצוג הוא הקוד – הסופי – של תוכנית המחשב); קיים גם ייצוג מחזורי (ולכן סופי במובן זה שאחרי כתיבת מספר סופי של תווים כל המידע הדרוש לייצוג כבר נכתב) באמצעות מושג מתמטי הנקרא "שברים משולבים"; ואפילו הביטוי "שורש שתיים" או הסימון 2√ הוא ייצוג סופי מסויים.

אבל אם כל פיתוח עשרוני אינסופי הוא מספר ממשי חוקי, אז עבור רובם המוחץ לא יהיה לנו ייצוג סופי כלשהי; זוהי טענה מתמטית וקיימת לה הוכחה. זה מעלה שאלות לא פשוטות בדבר קיומם של היצורים המוזרים הללו שאיננו מסוגלים לתת להם ייצוג סופי בשום דרך שהיא.

ההגדרה שנתתי כאן למספרים ממשיים אינה ההגדרה שאיתה מתמטיקאים עובדים בדרך כלל; ישנן הגדרות שונות ומדוייקות יותר ושאינן דורשות דיבור על עשר ספרות דווקא. לא אציג אותן כאן כי הן דורשות מושגים מתמטיים לא טריוויאליים, אך אספר שגם בהן קיימת אותה בעיה שהצגתי – האינסוף איכשהו מכניס את עצמו פנימה ומונע ייצוג סופי של רוב המספרים הממשיים.

למתמטיקאים אין בדרך כלל בעיה עם קיומם של היצורים הללו, והתועלת שהם מביאים למתמטיקה ולענפי המדעים השונים ובפרט פיזיקה היא אדירה; היקום שלנו מתואר באמצעות המספרים הממשיים, ועם זאת, חשוב לי להסב את תשומת לבכם לכך שדווקא אותם מספרים "ממשיים" הם אלו שהגדרתם היא המפוקפקת ביותר.

בחזרה ל-i

אחרי כל זה אנו שבים אל המספר הדמיוני i. אני מקווה שבשלב זה העובדה שאין מספר ממשי שהעלאה שלו בריבוע מחזירה מינוס 1, לא גורמת לכם לפסול את קיומו של i על הסף, ממש כשם שהעובדה שאין מספר רציונלי שהעלאה שלו בריבוע מחזירה 2 לא גרמה לכם לפסול את הממשיים על הסף. ובכל זאת, אם i איננו מספר ממשי, מה הוא כן?

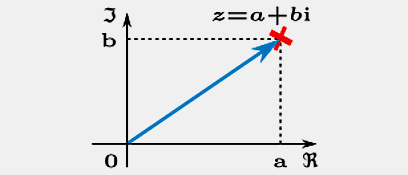
ראשית, בואו נזכור ש-i אינו לבד במשחק. אפשר לכפול אותו במספרים ממשיים ולחבר אליו מספרים ממשיים, ולקבל הרבה מאוד מספרים מהצורה a+bi כאשר a,b הם מספרים ממשיים. מספר כזה נקרא מספר מרוכב, והמספרים המרוכבים הם הכללה של המספרים הממשיים (כי אם b=0 נקבל מספר ממשי; ואת i עצמו נקבל אם a=0 ו-b=1).

מספרים מרוכבים

כעת, כפי שנאמר במאמר של באאז והוארטה, ניתן להשתמש במספרים המרוכבים כדי לתאר פעולות במישור - אלא שאפשר גם להפוך את הקערה הזו על פיה: אפשר להגדיר מספרים מרוכבים בתור זוגות של נקודות במישור!

נקודה במישור היא זוג של מספרים ממשיים: (a,b), ואפשר לחשוב על המספרים הממשיים ה"רגילים" כאילו הם מתחבאים על ציר ה-x במישור, כלומר המספר הממשי a מיוצג על ידי הנקודה (a,0).

אפשר לבצע על נקודות אלו פעולת חיבור פשוטה: (a,b)+(c,d)=(a+c,b+d). כלומר, מחברים כל קואורדינטה לחוד. אפשר היה לצפות שכפל יוגדר בצורה דומה – כל קואורדינטה לחוד – אבל ההגדרה שבה משתמשים היא מסובכת יותר, ובמבט ראשון לא הכי ברור מה הולך בה: (a,b)x(c,d)=(ac-bd,ad+bc).

זו לא הגדרה טבעית אלא אם היעד שלנו ברור לנו מראש, אבל – וזו הנקודה המרכזית שלי – זו הגדרה חוקית. אין חוק שמכריח אותנו להגדיר פעולה בשם "כפל" באופן שזהה לחלוטין לכפל של מספרים ממשיים. מי שמקבל את קיומם של מספרים ממשיים יתקשה להצדיק טיעונים נגד קיומם של זוגות של מספרים ממשיים, או היכולת שלנו להגדיר עליהם פעולות אריתמטיות שמעניינות אותנו.

כאן אתם יכולים להטיל ספק ולשאול: למה דווקא ההגדרה שאני נתתי היא ההגדרה הנכונה ל"כפל" של קואורדינטות? ובכן, ראשית קל לראות שמתקיים (a,0)x(b,0)=(ab,0).

כלומר, הכפל שהגדרנו, כשמסתכלים מה הוא מעולל למספרים ממשיים, אכן מתנהג כמו הכפל של ממשיים; ובאופן כללי אפשר לראות שהכפל והחיבור שהגדרתי עדיין מקיימים את החוקים שנלמדו בבית הספר היסודי – חוקי החילוף, הקיבוץ והפילוג. כך שגם אם ההגדרה שנתתי אינה הדרך היחידה להגדיר כפל על נקודות, זו עדיין הגדרה שנותנת לנו מערכת מספרים שמתנהגת יפה, ולא סתם בלאגן שרירותי.

בואו נראה מה קורה במקרה פרטי מסויים של הכפל, כשאנחנו כופלים את הנקודה (0,1) בעצמה: אנו מקבלים, כפי שאולי ניחשתם, (1,0-). כלומר, הנקודה (0,1) היא השורש של הנקודה (1,0-), אבל מה הן הנקודות הללו?

אם נצייר מערכת צירים, נוכל לצייר על גבי ציר x את ציר המספרים הרגיל שלנו. באופן זה, המספר הממשי a יהיה בעצם הנקודה (a,0) והנקודה (0,1) תהיה על גבי ציר y, הציר האנכי.

מה שאנו רואים הוא שהשורש של מינוס 1 אכן לא נמצא על ציר המספרים ה"רגיל" אלא על ציר שמאונך לו. אנחנו לא בדיוק "ממציאים" את המספר החדש i; אנחנו פשוט מרימים את הראש מציר המספרים החד-ממדי שלנו ורואים שיקום המספרים הוא רחב יותר מזה ומכיל ממדים נוספים, ואת המספר i אנו מחפשים ומוצאים בתור הנקודה (0,1) על הציר החדש שנוסף לעולם שלנו.

זוהי גם התשובה לשאלה מתחילת המאמר, מדוע המתמטיקאים אוהבים את המספרים המרוכבים. מבלי להיכנס כעת לדוגמאות מסובכות, העולם המתמטי פשוט יותר שלם איתם. אנחנו מסוגלים להבחין בתופעות שנסתרו עד כה מעינינו – כי הסתכלנו רק על ציר המספרים הממשי – כשאנחנו מתבוננים בהם בהקשר הרחב יותר של מספרים מרוכבים.

שימושים מרוכבים

המתמטיקאי המפורסם קארל פרידריך גאוס (הנחשב לאחד מגדולי המתמטיקאים בכל הזמנים) הוא שהפך את המספרים המרוכבים לפופולריים בתחילת המאה ה-19 כשהשתמש בהם בהכללות לאחד ממשפטיו המפורסמים ביותר - משפט ההדדיות הריבועית. גם כאן מדובר על תוצאה שעוסקת במספרים "רגילים" ולא ניתן להבינה עד הסוף מבלי להכניס את המרוכבים לתמונה.

אחריו, באמצע המאה ה-19, הגיע רימן והראה כיצד שאלות על פיזור המספרים הראשוניים ניתנות לתקיפה מכיוון בלתי צפוי לחלוטין: פונקציה ("פונקציית הזטא של רימן") שהערכים שהיא מקבלת ומחזירה הם מספרים מרוכבים, וניתנת להבנה בעזרת טכניקות חשבוניות לחקירת פונקציות במספרים מרוכבים שהכלילו את החשבון הדיפרנציאלי והאינטגרלי של ניוטון ולייבניץ שעסק במספרים ממשיים.

רעיונותיו של רימן הבשילו לבסוף למשפט שהוכח לקראת סוף המאה - "משפט המספרים הראשוניים" שנותן הערכה חזקה מאוד של "כמות" המספרים הראשוניים, אך הסיפור לא נגמר; ישנה תכונה מסויימת של הפונקציה שאם תוכח תגרור גירסה חזקה בהרבה של משפט המספרים הראשוניים. ההשערה כי תכונה זו מתקיימת נקראת "השערת רימן" והיא אחת מהבעיות הפתוחות המרכזיות במתמטיקה בימינו.

לתוצאות אלו ולתוצאות דומות רבות אחרות היה חלק חשוב בהכנסתם של המספרים המרוכבים לקונצנזוס המתמטי ולהתייחסות אל המספרים ה"דמיוניים" כממשיים לא פחות מהמספרים הממשיים. כיום מעטים הענפים המתמטיים שבהם לא מופיעים כלל מספרים מרוכבים.

מעבר לשימושיות של המספרים המרוכבים ולשאר טיעונים שכלתניים בזכותם של מספרים אלו, למתמטיקאים יש עוד סיבה פשוטה לחבב אותם: הם הופכים את המתמטיקה ליפה יותר. קשה להעריך זאת ממבט ראשון כשם שקשה להעריך יצירה מוזיקלית מורכבת או סרט קולנוע עתיר ניואנסים, אבל יש דוגמה צפויה אחת שחביבה גם עלי:

זהו מקרה פרטי של נוסחה שנתגלתה בידי אוילר בן המאה ה-18 (גם הוא מתמטיקאי דגול) וקושרת את המספרים הטבעיים הבסיסיים 0 ו-1 יחד עם המספר e (שהוא קבוע מתמטי חשוב ביותר שצץ במקומות רבים במתמטיקה ומסייע לחשב את הזמן שנדרש להתפרקות רדיואקטיבית, להתפלגות הגבהים של בני אדם שונים ולחישוב הרווח שמניבה ריבית דריבית), עם הקבוע המפורסם π ועם ידידינו i:

e בחזקת i π ועוד 1 = 0.

דעה רווחת היא כי זוהי "הנוסחה היפה במתמטיקה". לטעמי במתמטיקה העיקר אינו הנוסחאות (בניגוד לרושם השגוי שנוצר לעתים, נוסחאות אינן חלק מרכזי מהמתמטיקה), אך הנוסחה ללא ספק מקסימה ואף יותר מקסימה הסיבה שבגללה היא עובדת (כי מה זה בעצם אומר, להעלות מספר בחזקת i?). אך זה סיפור אחר ויסופר כבר בפעם אחרת.

גדי אלכסנדרוביץ' הוא בעל תואר שלישי במדעי המחשב ומחבר הבלוג "לא מדויק".