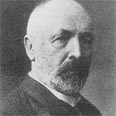משפטי אי השלמות של גדל: הטוב, הרע והיפה
קורט גדל זעזע את עולם המתמטיקה כשפרסם את המשפטים המפורסמים שלו בשנות ה-30 של המאה העשרים. על מה הייתה כל המהומה? גדי אלכסנדרוביץ' מסביר בלשון בני אדם את סוד קסמו של המשפט המתמטי בעל המוניטין המפוקפק
אם תבקשו ממני לנחש מהו המשפט המתמטי שצץ במספר הגדול ביותר של דיוני אינטרנט שלא קשורים למתמטיקה, אנחש שזהו משפט אי השלמות של גדל. אם תבקשו ממני לנחש בכמה מאותם דיונים המשפט אכן רלוונטי לדיון, אנחש שבמיעוט זניח.
למשפט יש מוניטין כפול מוזר למדי: בקרב מי שמבינים אותו הוא נחשב לתוצאה יפה ומעניינת אך ברוב תחומי המתמטיקה הוא אינו חשוב או מרכזי במיוחד ובוודאי שלא משפיע על עבודתם היומיומית של רוב המתמטיקאים.
בקרב מי שלא מבינים אותו המשפט זוכה לעתים לכתרים של רועץ המתמטיקה, ההוכחה האולטימטיבית לעליונות האדם על המכונה, לנימוק לקיום אלוהים ולנביא הפוסט-מודרניזם. אני מקווה שהמאמר הזה יסייע קצת לשינוי התדמית הזו של המשפט ויציב אותו באור נכון יותר.
קצת היסטוריה
בשלהי המאה ה-19 רעש וגעש העולם המתמטי סביב תורה חדשה שהמציא המתמטיקאי גאורג קנטור – תורת הקבוצות. תורת זו הציגה גישה חדשה ונועזת להתמודדות עם מושג האינסוף המתמטי: אחת מתוצאותיה הבסיסיות היא קיומם של סוגים שונים של אינסוף (למשל, אינסוף המספרים הטבעיים הוא אותו אינסוף כמו אינסוף המספרים הרציונליים, אך הוא אינסוף קטן יותר מאינסוף המספרים הממשיים).
מעבר לכך היא גם הציעה למתמטיקאים בסיס שעליו ניתן לבנות את יתר המתמטיקה – מושג ה"קבוצה" היה כה אלמנטרי עד שאת כל שאר המושגים המתמטיים (למשל, את כל סוגי המספרים) היה ניתן לתאר באמצעותו. אלא שלרוע המזל, תורת הקבוצות לא הייתה נטולת פגמים: התגלו בה מספר סתירות פנימיות (גם על ידי קנטור עצמו וגם על ידי אחרים) שהמפורסמת מביניהן היא "פרדוקס הספר" של ברטראנד ראסל.
"פרדוקס הספר" ניתן לניסוח פשוט כך: בעיר כלשהי יש ספר, שעל פי חוק מספר את כל התושבים שאינם מספרים את עצמם ורק אותם. לרוע המזל הספר איננו קירח ולכן נשאלת השאלה מי מספר אותו.
מצד אחד אם הספר מספר את עצמו אז על פי החוק אסור לו לספר את עצמו (הרי הוא מספר רק אנשים שאינם מספרים את עצמם), אבל אם הספר אינו מספר את עצמו אז על פי החוק הוא חייב לספר את עצמו! הפרדוקס נשמע כמו התחכמות מילולית, אך ראסל גילה אותו בניסוח מתמטי מדויק לחלוטין שהצביע על בעיה מהותית בתורת הקבוצות, וכל ספר בתורת הקבוצות כולל אזכור של הפרדוקס.
הפתרון לפרדוקסים של תורת הקבוצות היה הגדרה מחדש של מושג הקבוצה בצורה זהירה יותר. מתמטיקאים הציעו רשימה של תכונות שבאות לתאר מהי קבוצה. למשל: קיימת קבוצה ללא איברים; לכל קבוצה קיימת קבוצה שמכילה אותה; לכל שתי קבוצות קיימת קבוצה שמכילה את כל האיברים שלהן, וכדומה.
התכונות הללו מכונות אקסיומות. אנחנו רגילים אולי לחשוב על אקסיומות בתור "משהו שנכונותו מובנת מאליה ולא צריך להוכיח אותו", אך במתמטיקה מודרנית לא זה פירוש המילה. אקסיומה היא הנחת יסוד; זה לא אומר שהיא מובנת מאליה, אלא רק שאנחנו מוכנים לקבל אותה כדי להתחיל את המשחק המתמטי. זה אומר שבמתמטיקה מערכות של אקסיומות נמצאות תחת חשד תמידי – אולי האקסיומות לא טובות מספיק? אולי אחת מהן מיותרת? והחמור מכל – אולי מהאקסיומות הללו נובעת סתירה?
באקסיומות של תורת הקבוצות לא נתגלתה סתירה עד היום, אבל בתחילת המאה ה-20 כשזכר גילוי הפרדוקסים בתורת הקבוצות עוד היה טרי, המתמטיקאים רצו להבטיח לעצמם שמערכת האקסיומות שעליה הם מבססים את המתמטיקה תהיה נקיה מכל סתירה.
בפרט בלטה תוכניתו השאפתנית של המתמטיקאי דיוויד הילברט, שהיה גדול המתמטיקאים של אותה התקופה ומנהיג של כל העולם המתמטי. הילברט חיפש מערכת אקסיומות שבעזרתה ניתן יהיה להוכיח כל משפט מתמטי אפשרי.
יותר מכך: הוא רצה שתהיה הוכחה פשוטה לכך שמערכת האקסיומות הזו חופשיה מסתירות, והוא רצה שמערכת האקסיומות הזו תהיה פשוטה מספיק כדי שמחשב (מושג שלא היה קיים בזמנו של הילברט אך מתאר היטב את מה שהוא התכוון אליו) יוכל לבדוק את נכונותן של ההוכחות שהיא כוללת.
הילברט ראה בתוכנית הזו מבצע כביר, שאחריו תיפתר אחת ולתמיד בעיית היסודות של המתמטיקה: ניתן יהיה להגיד בודאות כמעט מלאה (עבור מתמטיקאים זה תמיד "כמעט"; בניגוד לאמונה פופולרית, אפילו במתמטיקה אין ודאות מוחלטת) שהמתמטיקה נקיה מפרדוקסים ובעיות; יותר מכך, אפשר יהיה, לפחות בתיאוריה, למצוא את כל המשפטים הנכונים במתמטיקה באמצעות מחשב שבכלל לא יודע מתמטיקה אבל מכיר את מערכת האקסיומות של הילברט.
מכאן אפשר להבין את ההפתעה (ואולי אף הזעזוע) שחווה העולם המתמטי כאשר בשנת 1931 פרסם מתמטיקאי אוסטרי צעיר בשם קורט גדל (Kurt Gödel) משפט שהראה כי מערכת האקסיומות הנפלאה של הילברט לא קיימת ואינה יכולה להתקיים.
משפט זה זכה לשם "משפט אי השלמות הראשון של גדל", מה שמרמז שיש גם משפט שני. אזכיר את השני (שהוא תוצאה מעניינת של המשפט הראשון) בהמשך, אך עיקר העניין שלי יהיה במשפט הראשון, שאותו אני מכנה בפשטות "משפט אי השלמות של גדל".
מערכות הוכחה
משפט גדל עוסק במערכות הוכחה, ומבלי להיכנס להגדרה מדוייקת שלהן, כל מערכת כזו כוללת שלושה מרכיבים עיקריים: שפה, אקסיומות וכללי היסק.
"שפה" היא מערכת מוסכמת של סימנים שבאמצעותם ניתן לכתוב טענות מתמטיות (למשל, הסימנים +, x, = ואחרים הם חלק מהשפה שנדרשת לנו כדי לתאר טענות על חשבון). החשיבות של שפה היא בכך שאם השפה לא עשירה מספיק, יהיו טענות מתמטיות שבכלל לא יהיו ניתנות לניסוח באמצעותה ולכן מערכת ההוכחה כלל לא תעסוק בהן.
אקסיומות, כפי שאמרתי קודם, הן פשוט אוסף טענות (שמנוסחות בשפה של מערכת ההוכחה) שאנו מניחים את נכונותן בלי הוכחה, פשוט כי צריך נקודת התחלה כלשהי. כללי היסק הם כללים שמאפשרים להסיק טענות חדשות מתוך טענות קיימות – למשל, מ"אם ירד גשם היום אני אקח מטריה" ו"יורד גשם היום" אפשר להסיק את "אני לוקח מטריה" (כלל היסק זה מכונה מודוס פוננס).
הוכחה במערכת כזו היא פשוט סדרה סופית של טענות שכתובות כולן בשפה של המערכת, כך שכל טענה היא או אקסיומה, או נובעת מטענות קודמות על ידי כללי ההיסק.
בבתי הספר נתקלים במערכת הוכחה שכזו בלימודי הגאומטריה של המישור. למעשה, העובדה שזו הזדמנות לעבוד עם מערכת הוכחה מתמטית "אמיתית" היא סיבה עיקרית לכך שלימודי הגאומטריה של המישור הם חשובים כל כך גם עבור מי ששונא גאומטריה.
הטענה האחרונה בסדרת הטענות של ההוכחה היא ה"מטרה" של ההוכחה, המשפט שההוכחה מוכיחה (אם כי בעצם כל טענה שמופיעה במהלך ההוכחה היא משהו שההוכחה מוכיחה).
שלמות, עקביות, אפקטיביות, אריתמטיות
מערכת הוכחה שבה ניתן להוכיח או להפריך כל טענה שניתן לנסח בשפה של מערכת ההוכחה נקראת שלמה. “להפריך" כאן פירושו פשוט "להוכיח את ההפך". למשל, הטענה "בכל משולש סכום שתיים מהצלעות גדול או שווה לזווית השלישית" היא טענה שניתן לנסח בשפה של הגאומטריה האוקלידית (שיודעת מה זה "משולש" ומה זו "זווית"), ואכן ניתן להוכיח אותה במסגרת הגאומטריה האוקלידית.
הטענה "כל משולש הוא שווה צלעות" לעומתה היא כמובן לא נכונה, והגאומטריה האוקלידית מפריכה זאת על ידי כך שניתן להוכיח בה את הטענה ההפוכה, “קיים משולש שאינו שווה צלעות".
אחת מהתכונות של הגאומטריה האוקלידית (בניסוח מודרני ומדויק, לו אחראי אלפרד טרסקי) היא שזו אכן מערכת הוכחה שלמה – כל טענה שאפשר לנסח בשפה של הגאומטריה האוקלידית אכן ניתנת להוכחה או להפרכה. אלא שהגאומטריה האוקלידית אינה מכסה את כל המתמטיקה, להבדיל מתורת הקבוצות שניתן להשתמש בשפה שלה כדי לנסח (ברמת העיקרון התאורטית, לפחות) כל טענה מתמטית.
ומה אם היה מתברר שאפשר היה להוכיח בגאומטריה האוקלידית את גם את הטענה "קיים משולש שאינו שווה צלעות" וגם את הטענה "כל המשולשים הם שווי צלעות"? במקרה הזה היינו אומרים שמערכת ההוכחה של הגאומטריה האוקלידית אינה עקבית.
מערכת עקבית היא כזו שבה לא ניתן להוכיח דבר והיפוכו – לא ניתן להגיע לסתירה. אם מערכת ההוכחה שלנו מוכיחה סתירה, המסקנה היא שהמערכת לא מתארת אף אובייקט מתמטי שמעניין אותנו, כי המתמטיקה אינה עוסקת באובייקטים שכוללים סתירות.
בנוסף, למערכות הוכחה לא עקביות יש בדרך כלל בעיה נוספת – ברוב מערכות ההוכחה כללי הגזירה הם כאלו שנובע מהם שאם ניתן להוכיח סתירה במסגרת המערכת, אז ניתן להוכיח כל טענה במסגרת המערכת – תוצאה זו מכונה "Principle of explosion”. מערכות הוכחה שבהן התכונה הזו מתקיימת הן באמת חסרות טעם – אם אפשר "להוכיח" הכל, לא סביר שיש משמעות מעניינת ל"הוכחה" במערכת שכזו.
הגאומטריה האוקלידית היא מערכת הוכחה פשוטה למדי – יש בה מספר סופי של אקסיומות, וכללי ההיסק בה גם הם אינם מורכבים. אפשר באופן עקרוני לכתוב תוכנית מחשב שקוראת הוכחות בגאומטריה האוקלידית ומוודאת את נכונותן (כלומר, שמה שמוצג כאקסיומה הוא באמת אקסיומה ושמה שמוצג כנובע ממשפטים קודמים אכן נובע מהם).
מערכת הוכחה שמקיימת את התכונה הזו – שאפשר לכתוב תוכנית מחשב שמוודאת נכונות הוכחות בה – נקראת אפקטיבית. כדאי להדגיש שכיום לא ידוע לנו שהאדם מסוגל לבצע חישובים שתוכניות מחשב אינן מסוגלות לבצע, כך שלמרות שאני מדבר על "ניתן לבדיקה בידי תוכנית מחשב", כל עוד לא הוצג טיעון משכנע מאוד לכיוון ההפוך, הכוונה היא גם ל"ניתן לבדיקה על ידי אדם". די ברור שיש משהו בעייתי מאוד במערכות הוכחה שלא ניתן לבדוק נכונות של הוכחות בהן, כך שדרישת האפקטיביות ממערכת היא חשובה למדי.
לסיום, מערכת הוכחה נקראת אריתמטית אם היא מסוגלת לתאר, בין היתר, את המספרים הטבעיים עם פעולות החיבור והכפל. זה אומר שהשפה של מערכת ההוכחה תצטרך להכיל את הסימנים המתאימים (בדרך כלל זה סימן ל-0, סימן לעוקב, וסימנים לחיבור וכפל) ואקסיומות מתאימות שמוודאות שהסימנים הללו אכן מתאימים להתנהגות הצפויה של מספרים טבעיים. בהיבט זה הגאומטריה האוקלידית נכשלת: היא איננה אריתמטית (וארחיב על כך קצת בהמשך).
כעת אפשר לתת ניסוח קומפקטי ומפוצץ למשפט אי השלמות של גדל: לא קיימת מערכת הוכחה מתמטית שהיא בו זמנית שלמה, עקבית, אפקטיבית ואריתמטית. מכיוון שארבע הדרישות הללו גם יחד חובקות את מה שהילברט ביקש למצוא, משפט גדל אכן מראה שהשאיפה של הילברט הייתה אופטימית מדי. אבל זה לא מרסק את המתמטיקה. ממש לא.
בחלק הבא אסביר כיצד מוכיחים את המשפט (לטעמי, זהו החלק המעניין בו באמת, וגם זה שהשפיע באופן מהותי על התפתחותם של מדעי המחשב התיאורטיים), וגם אומר משהו על מה המשפט איננו.
גדי אלכסנדרוביץ' הוא בעל תואר שלישי במדעי המחשב ומחבר הבלוג "לא מדויק".
לפנייה לכתב/ת 
