איך עובדת (ומה היא) קוביה אלקטרונית?
יש שחקנים שבמקום להטיל קוביות אמיתיות, נעזרים בקוביית פלסטיק עם נורות לד שבכל הטלה מוציאה מספר אקראי אחר. איך זה עובד?
הגאדג'ט שיונח השבוע תחת מברג המנתחים הוא צעצוע אלקטרוני פשוט ותמים למראה: קוביה עם תא סוללות בצד אחד, ולוח בצד השני שעליו שש נוריות LED אדומות. כאשר מטלטלים את הקוביה הזו מספיק חזק, או מטילים אותה על משטח קשיח, היא מציגה (בסיומו של רצף הבהובים וצפצופים שכואב בעיניים ובאוזניים) מספר אקראי למשך מספר שניות. ללא ספק, פתרון מעולה למי שמעדיף לשחק שש-בש בחושך.
מבחינה טכנולוגית, אם כן, לא מדובר בהתקן מורכב במיוחד – אך הקוביה הצנועה הזו יכולה להדגים כמה עקרונות טכנולוגיים מעניינים. עם זאת, לפני שניגע בתיאוריה, בואו נראה איך הקוביה עובדת בפועל, ונפרק אותה לחתיכות.
אחד הדברים הראשונים שבולטים לעין, בבחינה מקרוב, הוא הקפיץ העדין שמסתתר לצד נוריות ה-LED ואשר אחד מקצותיו מרחף באוויר מעל פס מתכת. זהו חיישן רעידות זול, שמזכיר קצת את זה שראינו בצעצוע המנגן. בהינתן תנועה חדה מספיק, הקצה החופשי של הקפיץ מתנודד בפראות ויוצר מגע עם פס המתכת. הדבר סוגר מעגל חשמלי וגורם למיקרו-בקר הפנימי להתחיל את רצף בחירת המספר. קפיץ כזה קיים, אגב, בכל הצעצועים הזולים שנמכרים בדרך כלל ביום עצמאות ומאירים ומנצנצים לזמן מסוים בתגובה לטלטול.
הפלוס שבמינוס
שתי סוללות הכפתור, כל אחת מהן במתח 1.5 וולט, מספקות ביחד את 3 הוולטים הדרושים למיקרו-בקר, לרמקול המצפצף ולתאורה – ולמעשה, אלה כל הרכיבים החשמליים שיש בקוביה, והם מחוברים זה לזה בלוח מודפס בסיסי. הלוח מוצג בתמונה הבאה מימין, והקווים הצהובים בעותק שמשמאל מדגישים אזור מוליך חשמל שמשותף לכל נוריות ה-LED. לכל נורית שתי רגליים, לפלוס ולמינוס חשמליים, והאזור הנ"ל מחבר את כל רגלי הפלוס ישירות לסוללה.
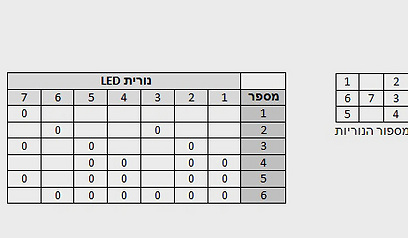
נשאלת השאלה, למה דווקא הפלוס? הרי ברוב המקרים, מקובל לחבר את הרכיבים השונים במעגל דווקא למינוס משותף (אדמה). אם נסתכל על רגלי המינוס של נוריות ה-LED, נראה שכל אחת מהן מחוברת לפס מוליך נפרד, וכל הפסים מגיעים אל מתחת לגוש הפלסטיק השחור. כלומר, מסתתר שם מיקרו-בקר, "ג'וק" קטן וחכם, ששבע מהרגליים שלו מוקדשות לשליטה בנוריות ה-LED ולהצגת המספרים 1-6 כנקודות מוארות על הקוביה. דבר כזה מבוצע בדרך כלל באמצעות טבלת המרה ששמורה בזיכרון הג'וק, וקובעת – עבור כל מספר – אילו רגליים מבין אלה שמחוברות לנוריות ה-LED יהיו במצב של מתח גבוה (3 וולט, במקרה שלנו) ואילו מהן במצב "אדמה" (0 וולט). בגלל הסידור הייחודי שראינו, מתח גבוה כאן פירושו שהנורית דווקא לא תדלוק: שתי הרגליים שלה יהיו באותו מתח ולכן לא יהיה שום זרם, כפי שכדור, למשל, לא מתגלגל לשום צד בצינור מאוזן לגמרי. דווקא המתח הנמוך הוא זה שיגרום ל"שיפוע", להפרש פוטנציאלים – ולהידלקות הנורית.
אילו רגלי הפלוס של נוריות ה-LED היו מחוברות לרגלי הג'וק, הוא זה שהיה צריך לטפל באספקת ותיעול הזרם החשמלי לכל אחת מהן. מכיוון שמדובר כאן על ג'וק קטן ועדין למראה, יש סיכוי טוב שמדובר בדרישה מוגזמת עבורו. בסידור הקיים, מכיוון שהוא בסך הכל פותח "ניקוז" עבור רגל המינוס, הסוללה היא זו שנותנת את הזרם הדרוש, ואילו המיקרו-בקר יכול להמשיך לעבוד בכיף עם זרמים זעירים כמו שהוא רגיל. זו, בכל אופן, ההשערה שלי – אם יש אלקטרונאי בקהל שיכול לאשר או להפריך אותה, בכיף.
הצעת ייעול
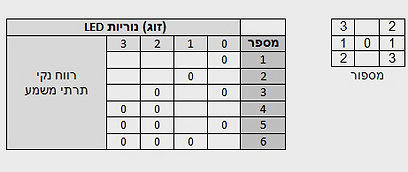
מכיוון שהקוביה בסך הכל עושה היטב את המצופה ממנה, אי אפשר להתלונן על התכנון הזה בן שבע הרגליים. עם זאת, רק בשביל התרגיל המחשבתי, בואו נראה איך אפשר היה לשפר אותו – למשל, תוך ניצול של ארבע רגלי ג'וק בלבד במקום שבע. אם נסתכל שוב על הטבלה למעלה, אפשר לראות שהנוריות 3 ו-6 הן זוג: בכל מספר שנבחר, המצב של האחת זהה למצב של השניה. גם 1 ו-4 הן זוג, וגם 2 ו-5. אם נחבר כל זוג כזה לרגל יחידה של המיקרו-בקר, נוכל לפנות כך שלוש רגליים לשימושים אחרים. החיבורים והטבלה ייראו בערך ככה:
לא אקראי ולא במקרה
הקוביה מציגה בכל פעם ערך אקראי – לפחות ככה זה נראה. איך היא עושה את זה? איך ג'וק, שהוא מין מחשב זעיר שמריץ אך ורק פקודות מוכתבות מראש, מסוגל "להמציא" רצף של מספרים אקראיים, שמהיותם אקראיים לא אמורים להיות מוכתבים מראש בשום אופן?
במחשבים רגילים נהוג להשתמש ב"מחולל מספרים פסודו-אקראיים": נוסחה מתמטית שעם הפרמטרים הנכונים, מפיקה רצף של מספרים שצופה רגיל מבחוץ לא יכול לנחש מראש. בדרך כלל, נוסחאות כאלה עובדות עם מספרים גדולים, והמחשב מחזיר למשתמש רק חלק מכל מספר (למשל, באמצעות חישוב השארית מחילוק תוצאת הנוסחה ב-32,768). התוצאה של כל חישוב מוזנת לחישוב הבא, וזה מבטיח שהתוצאות לא יהיו מחזוריות בטווח המעשי.
לרוע המזל, הנוסחה הזו צריכה להתחיל מאיפשהו, ואם תנאי ההתחלה שלה יהיו זהים גם רצף המספרים ה"אקראיים" שיתקבל יהיה זהה (כפי שהדגמתי בעבר במקום אחר). אם שמתם לב, בסרטון למעלה, ניתקתי את הסוללות לקוביה – מה שאמור "לאפס" את המיקרו-בקר – וחיברתי מחדש, אך רצף התוצאות לא חזר על עצמו. אז אם מדובר במחולל מספרים אקראיים מתמטי, מה גורם לתנאי ההתחלה שלו להשתנות?
יש מספר דרכים לדאוג שהרצף האקראי, או האקראי-לכאורה, לא יחזור על עצמו אפילו בהתקן פשוט כמו הקוביה. לדוגמה, אפשר לדאוג שהמיקרו-בקר יספור אלפיות (או מיליוניות) שניה מרגע האתחול שלו, או מאז בחירת המספר הקודמת, ועד למגע הראשון של הקפיץ בפס המתכת. הסיכוי שמשתמש אנושי כלשהו יצליח לכוון את הטלת הקוביה בדיוק של אלפית השניה הוא אפס, ולכן מספיק להוציא שארית מחלוקת המונה הזה בשבע, ויש לנו תוצאה אקראית להפליא בכל פעם מחדש.
אופציה נוספת היא להיעזר ברגל של ג'וק שמסוגלת לתפקד כחיישן מתח חשמלי. זוהי פונקציה סטנדרטית לגמרי במיקרו-בקרים רבים, ואחד הדברים המעניינים בה הוא שאם הקלט "צף", כלומר שהרגל אינה מחוברת למקור מתח או ל"אדמה", נרשם בה רעש לבן. גם הרעש הזה אינו מתוכנן או צפוי, ואפשר לגזור ממנו מספרים אקראיים לתצוגה.
אפשרות שלישית היא לעבוד עם הנוסחה המתמטית בלבד, בלי למדוד זמן או קלט חיצוני, ופשוט לשמור את התוצאה של כל הטלה באזור בזיכרון, שאינו נמחק בזמן האיפוס. הרבה דגמים של מיקרו-בקרים מצוידים בכמה מאות בייטים של זיכרון EEPROM, שהערכים בו נשארים ויהי מה עד שכותבים עליהם משהו אחר. זהו זיכרון איטי מדי לפעולה שוטפת, וגם אורך החיים שלו מוגבל לרוב למשהו כמו 10,000 כתיבות, אך לשמירה של תוצאת הטלת קוביה ושחזורה בעת האתחול, הוא מתאים כמו כפפה ליד.
